Beating Wave Experiment
Introduction
The Beating Wave Experiment (BWX) investigates what is potentially a very efficient method of energizing (or heating) plasma with electrostatic (ES) waves. One area of application for such a heating mechanism is in plasma propulsion. However, before any specific application is found, it is essential to investigate and understand the fundamentals of the wave-particle interaction.
Electromagnetic waves and plasma interact in a complex manner. To simplify the analysis, it is often assumed that the wave amplitude is small-linearity approximation. Unfortunately, beating electrostatic wave-ion heating is fundamentally a non-linear mechanism. One can’t obtain an exact solution to the ion motion during ES heating.
Furthermore, most (but not all) studies focus on resonant types of wave-plasma interaction. A good analogy to the resonant interactions in plasma is the famous example how soldiers marching in step over a bridge caused the bridge to collapse. Another analogy is a surfer trying to catch waves. If he simply floats in the water it will not work. However if he pedals a little and matches his speed to that of the wave, he will ride the wave.

In a plasma, one example of resonant interaction is a phenomenon known as Landau damping where charged particles with velocities close to the phase velocity of the propagating wave, \(v_p = \omega_k\), are accelerated/slowed until their velocity becomes equal to the wave’s phase velocity.
An important application of resonant plasma heating is called Ion Cyclotron Resonance Heating (ICRH). Here, an electromagnetic circularly polarized wave is launched into the plasma such that some ions are rotating nearly in resonance with the wave. Once the resonance ions are accelerated by the wave, they transfer the energy they gained from the wave to other ions in the plasma via collisions.
As opposed to resonant phenomena, the interaction that is being studied in the Beating Wave Experiment is a non-resonant type of wave-plasma interaction. During this type of interaction an electrostatic beating wave “creates” resonance broadening - there is no single resonance. Many more ions are affected by the beating wave. This type of interaction has been observed to take place in the ionosphere [1], and is suspected to cause some instabilities in fusion devices.
Theoretical Investigations

To simplify our analysis we will make the following assumptions. First, we will assume that the plasma is fully ionized and the ion collision frequency is negligible. This assumption is not true in our experiment. A way to introduce a finite collision frequency into this simple model will be discussed later. Second, we assume that the electrostatic waves propagate perpendicularly to the magnetic field. This assumption is valid for electrostatic waves in plasma.
We begin by describing a single ion of mass \(m\), and charge \(q\) gyrating in a constant magnetic field of magnitude \(B\) oriented in z-direction.
The ion will execute cyclic motion at a gyro frequency:
\(\omega_c = \frac{qB}{m},\)
at a Larmor radius \(r_L\):
\(r_L = \frac{v}{\omega_c},\)
where \(v\) is the ion transverse velocity. Since \(\omega_c\) is constant we can directly
correlate any change in the Larmor radius to the changes in the ion velocity.
Electrostatic waves propagate x–direction. (For clarity only one wave is shown in the picture.) Using Lorentz equation (or alternatively Hamiltonian formulation) we could derive the equation of motion for the ion:
\[ \frac{d^2x}{dt^2} + \omega^2 x = \frac{q}{m}\sum_i E_i \cos(k_i x -\omega_i t).\]
Here \(E_i\), \(k_i\), and \(\omega_i\) are the amplitude, wave number, and wave frequency of the i-th wave.
Equally valid way to describe this system is to write down the Hamiltonian in action-angle coordinates: \[ H = \frac{\rho^2}{2} + \sum\frac{\epsilon_i}{k_i} \sin(k_i\rho\sin\theta - v_i\tau), \] where \(H\) is the Hamiltonian, \(\epsilon_i = k_1 q E_i / m \omega^2_c\), \(k_i = k_i/k_1\), \(r=k_1 x \sin q\), \(n_i = \omega_i / \omega_c\), \(\tau = \omega_c t\), and \(t\) is the angle measured clockwise from the y-axis. The process of normalizing the equation of motion to the action-angle coordinate system is described in many books on nonlinear dynamics including Refs. [2-4]. Physically, one can interpret \(r\) as the normalized Larmor radius, \(n_i\) as the normalized wave frequency, and \(e_i\) as the normalized wave amplitude.
To arrive to the case of the nonlinear beating wave-ion interaction we reduce the above given equation to two waves. To simplify our analysis even further, we assume that the waves are of equal magnitude and have the same wave number.
As the above equations are nonlinear in \(x\), no exact analytical solutions exist. The best we can do is to solve the equation numerically or seek an approximate solutions using perturbation theory. The solutions are then graphed as Poincare sections [5].
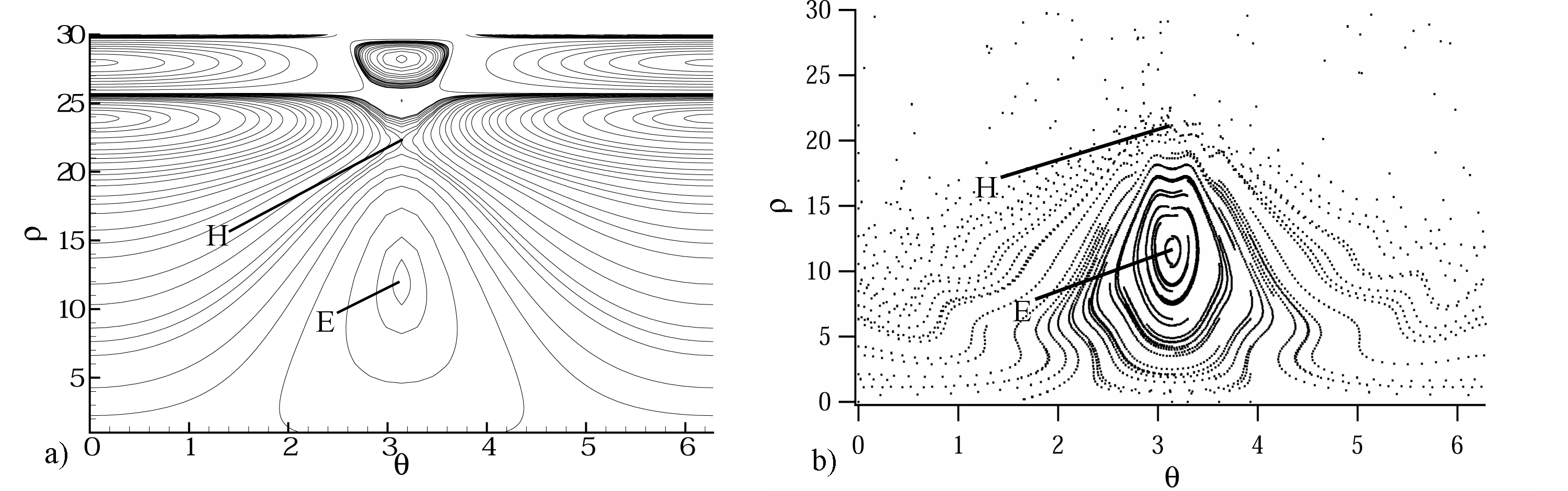
The figures above show typical Poincare sections for nonlinear beating wave - ion interaction. The section on the right was obtained by solving the Hamiltonian analytically using 2nd order Lie transformations [5]. Figure on the left was obtained numerically using Simplectic Integration Algorithm (SIA4) [6]. You can see that both figures agree with each other pretty well… with one exception. The analytical solution does not predict the existence of the stochastic (random) region – indicated by random points in the upper part of the right phase diagram.
In the past few years of working on the theoretical model we were able to derive the sufficient and necessary
conditions for ion acceleration by beating electrostatic waves using the phase diagram approach.
We were able to show that the Hamiltonian as well as the wave frequencies determine the condition for ion acceleration:
\[
\omega_i-\omega_j = n\omega_c\
\]
\[
H(v,\theta) > H_H(v_H,\theta_H)\
\]
\[
v_H \approx \frac{\omega}{k}, \theta_H = \pi
\]
Introducing collisions into the theoretical model complicates the model even further (remember, so far we were ignoring collisions in our model). An alternative way to deal with collisions is to write a Monte Carlo code [7]. This approach is explained in the next section.
Numerical Investigations
Solving the equation of motion
Numerical solutions provide us with a useful way of analyzing ion dynamics during wave – ion interaction. However, as was mentioned in the previous section, analytical solutions are only valid for small wave amplitudes. Speaking more precisely, the perturbation analysis used to obtain analytical solutions is only valid for small perturbation strength. In addition, analytical solutions will predict random (stochastic) motion.


On the other hand, numerical solutions, are valid for all wave amplitudes and do show the rich variety of dynamical behavior displayed by ions during the interaction. Also, a numerical solver provides us with an easy way to do the parametric studies of the phenomena. For example, we can investigate how variation in the wave amplitude affect the solution.
The above plots of angle versus normalized Larmor radius at 3 different wave amplitudes show the results of such an investigation. We can see clearly that when the wave amplitude is increased, the region of stochastic motion reaches lower values of velocity, r. Since stochastic acceleration is much faster than regular, that means that as the wave amplitude is increased the ions will be heated more and more efficiently.
While 4th order Runge-Kutta method could be used to solve the equation of motion to obtain the Poincare sections, we use a more accurate method known as 4th order Simplectic Integration Algorithm (SIA4) [6]. Relying on the conservation of the autonomous Hamiltonian [8], this method is specifically tailored for these types of problems.
Monte Carlo algorithm for collisions

The previous discussion relates to solving for the motion of a single magnetized charged particle interacting with a spectrum of beating electrostatic waves. In the previous discussion collisions were completely ignored. Now we add collisions through Monte Carlo techniques. In this method we assume that between collisions each particle moves according to the nonlinear equation of motion, as described beforehand. To calculate the change in the velocity during elastic collisions, such as Coulomb collisions, we use a Monte Carlo scheme similar to the one described in references [7], [9], and [10]. After the velocities of all the particles are updated, the particles are allowed to move according to the nonlinear equation of motion (which is again solved either using 4th order Runge-Kutta or Simplectic Integration Algorithm).
Monte-Carlo numerical simulations indicate that collisions actually improve heating efficiency during wave – ion interaction, contrary to some expectations. The figure to the left shows the energy evolution of the system of 1000 ions. SEW refers to the case of a single electrostatic wave, while BEW is the case of the beating electrostatic wave.
Experimental Investigations

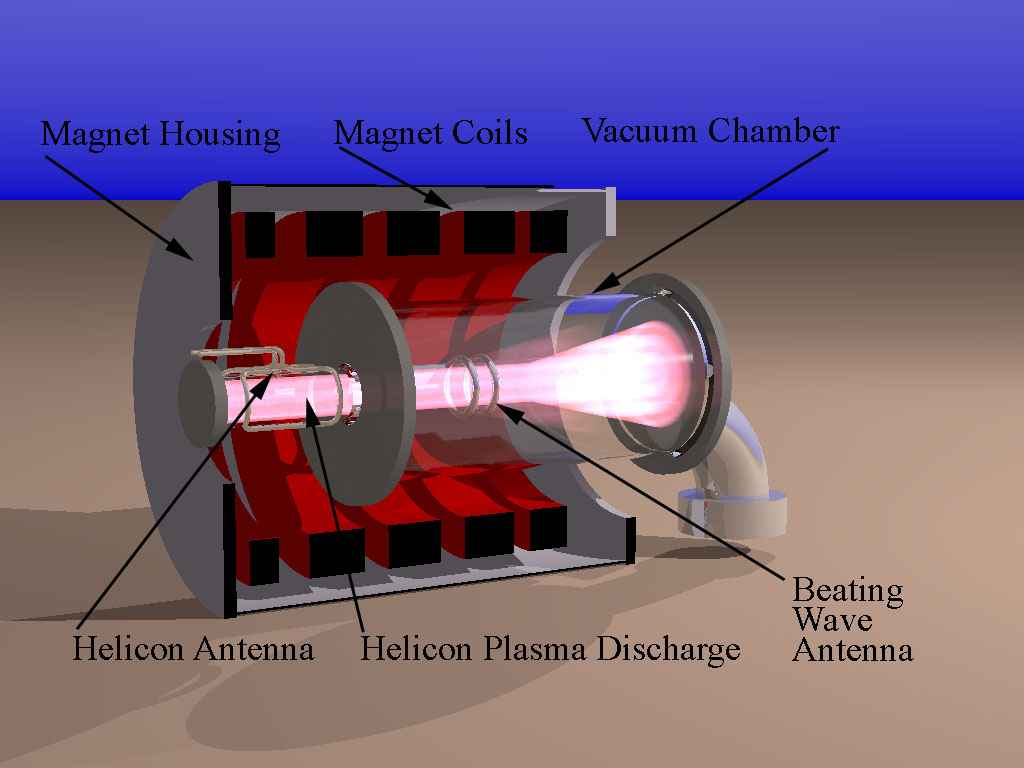
The experimental apparatus consists of a vacuum chamber comprised of two coaxial Pyrex cylinders connected by an aluminum plate (See the figures above). The small cylinder is 6 cm in diameter and 25 cm in length while the large cylinder is 20 cm in diameter and 45 cm in length. The cylinders are connected by an aluminum plate with a 6 cm concentric whole at the center to allow free flow of gas between the two cylinders.
The vacuum is maintained by mechanical and a 150 l/s turbo-molecular pump system. A base pressure of the order of 10-6 Torr is achieved. The vacuum chamber is located inside magnetic coils, which are able to produce up to 0.1 Tesla constant magnetic field parallel to the axis of the vacuum chamber. The chamber is backfilled with Argon to pressures ranging from 1-50 mTorr.
A Boswell type saddle antenna, used to produce helicon discharges, is placed around the small cylinder. The antenna is made of copper tubing to allow water-cooling during operation. The helicon discharge is produced by supplying power to the antenna from an ENI 13.56 MHz 1.2 kW power supply through a tuner. The tuner consists of an L network made of two Jennings 1000 pF 3 kV variable vacuum capacitors. It was placed as close to the antenna as possible to maximize coupling. Once the discharge is ignited in the small cylinder, the plasma propagates along the magnetic field lines, which are parallel to the axis of the cylinders, into the large chamber where the beating waves are launched.
Plasma diagnostics, such as RF compensated Langmuir probe and Retarded Potential Analyzer are located inside the large cylinder and can be moved axially as well as radially. A single electrostatic wave with frequency ~wc could be launched perpendicularly to the magnetic field by a set of double coils placed outside the large cylinder. The coils are placed in the Helmholtz coil configuration with the axis perpendicular to the axis of the vacuum chamber. The investigation of ion heating as well as the dispersion of this wave is currently under way.
The future studies involve launching beating electrostatic waves and studying their effect on ion heating.
References
- Ram, A.K., Bers, A., and Benisti, D., Ionospheric ion acceleration by multiple electrostatic waves., J. Geophys. Res. 103, 9431 (1998)
- E.Y. Choueiri and R. Spektor. Coherent ion acceleration using two electrostatic waves. Presented at the 36th AIAA Joint Propulsion Conference, Huntsville,AL, July 16-20, 2000. AIAA-2000-3759.
- R. Spektor and E.Y. Choueiri. Ion acceleration by beating electrostaticwaves: Criteria for regular and stochastic acceleration. Presented at the 27th International Electric Propulsion Conference (IEPC), Pasadena, California October 14-19, 2001. IEPC-01-209.
- R. Spektor and E.Y. Choueiri. Design of an Experiment for Studying Ion Acceleration by Beating Waves. Presented at the 37th AIAA Joint Propulsion Conference, Indianapolis, Indiana July 7-10, 2002. AIAA-2002-3801.
- A.J. Lichtenberg and M.A. Lieberman. Regular and Stochastic Motion, volume 38 of Applied Mathematical Sciences. Springer-Verlag, New York, 1983.
- R. Candy and W. Rozmus. A symplectic integration algorithm for separable hamiltonian functions. J. Comp. Phys., 92:230, 1991.
- Ping-Kun CHia, L. Schmitz, R.W. Conn. Effect of elastic scattering on stochastic ion heating by electrostatic waves. Phys. Plasmas 3 (5), may 1996, 1569-1577.
- H. Goldstein. Classical Mechanics. Addison-Wesley, Cambridge, MA, 1951.
- T. Takizuka and H. Abe. A Binary Collision Model for Plasma Simulation with a Particle Code. J. Comp. Physics 25, 205 (1977)
- Kenichi Nanbu. Probability theory of electron-molecule, ion-molecule, molecule-molecule, and Coulomb collisions for particle modeling of materials processing plasma and gases. IEEE transactions on plasma science, vol. 28, No 3, june 2000
Contact
Former students- Ben Jorns
- Slava Spektor
